Apprentice Chef, Inc.: Regression-based Analysis
Apprentice Chef, Inc.: Regression-based Analysis
By: Sophie Briques
Hult International Business School
Jupyter notebook and dataset for this analysis can be found here: Portfolio-Projects
Introduction
The meal kit market is competitive, with new players joining every day, as well as traditional grocery stores which are now also offering customers semi-prepared kits (Forbes, 2018). However, research shows consumers continue to order meal kits due to health reasons and getting to know new recipes (Nielsen, 2017).
Therefore, it is essential to understand the behaviors of our customers at Apprentice Chef which contribute to revenue to stay competitive.
Overview
- Best performing model was a Linear Regression with 15 features with a test score of 0.8279 and a cross validation score with 11 folds at 0.8076
- Optimal features were found using regularization methods such as Lasso and ARD Regression
- It is predicting the log of revenue, therefore when interpreting coefficients, it is important to transform back using 10(coef)
Case - Apprentice Chef, Inc.
Audience: Top Executives
Goal: understand how much revenue to expect from each customer within their first year of orders
Target consumer: busy professional, little to no skills in the kitchen
Product: daily-prepared gourmet meals delivered
Channels: online platform and mobile app
Revenue: 90% of revenue comes from customers that have been ordering for 12 months or less
Specifications:
- at most 30 min to finish cooking
- disposable cookware
- delicious and healthy eating
Data and Assumptions
Dataset:
2,000 customers (approx.)
- at least one purchase per month for a total of 11 of their first 12 months
- at least one purchase per quarter and at least 15 purchases through their first year
- dataset engineering techniques are statistically sound and represent the customers
Assumptions:
- all average times are in seconds
- revenue = price x quantity, where quantity is total meals ordered
- when customers attend master classes, they are looking to increase their cooking skills
Analysis Outline:
- Part 1: Exploratory Data Analysis
- Part 2: Transformations
- Part 3: Build a machine learning model to predict revenue
- Part 4: Evaluating Model
Set-up
# Importing Necessary Libraries
import pandas as pd # data science essentials
import matplotlib.pyplot as plt # essential graphical output
import seaborn as sns # enhanced graphical output
import statsmodels.formula.api as smf # regression modeling
from sklearn.model_selection import train_test_split # train test split
from sklearn.neighbors import KNeighborsRegressor # KNN for Regression
from sklearn.preprocessing import StandardScaler # standard scaler
from sklearn.linear_model import LinearRegression # linear regression (scikit-learn)
from sklearn.model_selection import cross_val_score # cross-validation
import sklearn
import numpy as np
# setting pandas print options
pd.set_option('display.max_rows', 500)
pd.set_option('display.max_columns', 500)
pd.set_option('display.width', 1000)
# specifying file name
file = "Apprentice_Chef_Dataset.xlsx"
# reading the file into Python
original_df = pd.read_excel(file)
chef_org. = original_df.copy()
User-defined functions
In the next section, we’ll design a number of functions that will facilitate our analysis.
## User-Defined Functions
# Defining function for distribution histograms
def continuous_distributions(variable, data, bins = 'fd', kde = False, rug = False):
"""
This function can be used for continuous variables.
PARAMETERS
----------
variable : str, continuous variable
data : DataFrame of the response and categorical variables.
bins : argument for matplotlib hist(), optional. If unspecified, Freedman–Diaconis rule is used.
kde : bool, optional, plot or not a kernel density estimate. If unspecified, not calculated.
rug : bool, optional, include a rug on plot or not. If unspecified, not shown.
"""
sns.distplot(data[variable],
bins = bins,
kde = False,
rug = rug,
color = 'g')
plt.xlabel(variable)
plt.tight_layout()
plt.show()
# Defining function to flag high outliers in variables
def outlier_flag_hi(variable, threshold, data):
"""
This function is used to flag high outliers in a dataframe the variables'
outliers by creating a new column that is preceded by 'out_'.
PARAMETERS
----------
variable : str, continuous variable.
threshold : float, value that will identify where outliers would be.
data : dataframe, where the variables are located.
"""
# creating a new column
data['out_' + variable] = 0
# defining outlier condition
high = data.loc[0:,'out_' + variable][data[variable] > threshold]
# imputing 1 inside flag column
data['out_' + variable].replace(to_replace = high,
value = 1,
inplace = True)
# Defining function to flag high outliers in variables
def outlier_flag_lo(variable, threshold, data):
"""
This function is used to flag low outliers in a dataframe the variables'
outliers by creating a new column that is preceded by 'out_'.
PARAMETERS
----------
variable : str, continuous variable.
threshold : float, value that will identify where outliers would be.
data : dataframe, where the variables are located.
"""
# creating a new column
data['out_' + variable] = 0
# defining outlier condition
low = data.loc[0:,'out_' + variable][data[variable] < threshold]
# imputing 1 inside flag column
data['out_' + variable].replace(to_replace = low,
value = 1,
inplace = True)
# Defining function for relationship scatterplots
def scatterplots(independ_var, target_var, data, color = 'g'):
"""
This function can be used for continuous variables
PARAMETERS
----------
independ_var : str, continuous variable
target_var : str, continuous variable we are trying to predict
data : DataFrame of the response and categorical variables.
color : str, optional. If unspecified, green color is used.
"""
sns.scatterplot(x = data[independ_var],
y = data[target_var],
color = color)
plt.xlabel(independ_var)
plt.tight_layout()
plt.show()
# Defining function to flag higher variables
def higher_change_flag(variable, index, threshold, data):
"""
This function is used to flag in a dataframe the variables' trend changes above a threshold by creating
a new column that is preceded by 'change_'.
PARAMETERS
----------
variable : str, continuous variable.
threshold : float, value that will identify after which the trend on variable y changes
data : dataframe, where the variables are located.
"""
new_column = 'change_' + variable + "_" + str(index)
# creating a new column
data[new_column] = 0
# defining outlier condition
high = data.loc[0:,new_column][data[variable] > threshold]
# imputing 1 inside flag column
data[new_column].replace(to_replace = high,
value = 1,
inplace = True)
# Defining function to flag change at variables
def at_flag(variable, index, threshold, data):
"""
This function is used to flag in a dataframe the variables' trend changes at a threshold by creating
a new column that is preceded by 'change_'.
PARAMETERS
----------
variable : str, continuous variable.
threshold : float, value that will identify after which the trend on variable y changes
data : dataframe, where the variables are located.
"""
new_column = 'change_' + variable + "_" + str(index)
# creating a new column
data[new_column] = 0
# defining outlier condition
high = data.loc[0:,new_column][data[variable] == threshold]
# imputing 1 inside flag column
data[new_column].replace(to_replace = high,
value = 1,
inplace = True)
Part 1: Exploratory Data Analysis (EDA)
Let us first take a look at our dataset and its dictionnary.
# Printing information on our dataset and its columns
# pulling up data dictionary
chef_description = pd.read_excel('Apprentice_Chef_Data_Dictionary.xlsx')
# Displaying:
chef_description
chef_org.info()
chef_org.describe()
Observations:
- Data types are coherent with each variable description
- 47 missing values in Family Name
- Number of observations: 1946
- Total of 28 variables (including target variable) where:
- 3 are floats
- 22 are integers
- 4 are objects
Step 1: Classifying our variables based on variable types:
categorical = ['CROSS_SELL_SUCCESS',
'MOBILE_NUMBER',
'TASTES_AND_PREFERENCES',
'PACKAGE_LOCKER',
'REFRIGERATED_LOCKER']
continuous = ['REVENUE',
'AVG_TIME_PER_SITE_VISIT',
'FOLLOWED_RECOMMENDATIONS_PCT',
'AVG_PREP_VID_TIME',
'LARGEST_ORDER_SIZE',
'MEDIAN_MEAL_RATING',
'AVG_CLICKS_PER_VISIT']
counts = ['TOTAL_MEALS_ORDERED',
'UNIQUE_MEALS_PURCH',
'CONTACTS_W_CUSTOMER_SERVICE',
'PRODUCT_CATEGORIES_VIEWED',
'CANCELLATIONS_BEFORE_NOON',
'CANCELLATIONS_AFTER_NOON',
'MOBILE_LOGINS',
'PC_LOGINS',
'WEEKLY_PLAN',
'EARLY_DELIVERIES',
'LATE_DELIVERIES',
'MASTER_CLASSES_ATTENDED',
'TOTAL_PHOTOS_VIEWED']
Step 2: Investigating missing values
# Inspecting missing values
chef_org.isnull().sum()
chef_org.loc[:,:][chef_org['FAMILY_NAME'].isna()]
Observations:
- Customers that have NA family name have parenthesis in names
- Parenthesis seem to indicate either their role or their geographical location
- Emails take the same format for last name
Conclusion: not enough information to impute last name, leave as NA and flag where they are since last name is a discrete variable that most probably will not bring insights to the purpose of this analysis.
# Flagging missing variables for FAMILY_NAME
# creating a copy of dataframe for safety measures
chef_m = chef_org.copy()
# creating a new column where 1 indicates that observation has a missing family name
chef_m['m_FAMILY_NAME'] = chef_m['FAMILY_NAME'].isnull().astype(int)
Step 3: Categorical Variables - Sample Size Check.
We need to see if the size of each of the categories is large enough to infer statistical significance or insignificance. If not, the variable could be insignificant to predict revenue when in reality its sample size is too small.
# Printing value counts for categorical variables
for variable in chef_org:
if variable in categorical:
print(f"""{variable}
------
{chef_org[variable].value_counts()}
""")
"""
CROSS_SELL_SUCCESS
------
1 1321
0 625
Name: CROSS_SELL_SUCCESS, dtype: int64
MOBILE_NUMBER
------
1 1708
0 238
Name: MOBILE_NUMBER, dtype: int64
TASTES_AND_PREFERENCES
------
1 1390
0 556
Name: TASTES_AND_PREFERENCES, dtype: int64
PACKAGE_LOCKER
------
0 1255
1 691
Name: PACKAGE_LOCKER, dtype: int64
REFRIGERATED_LOCKER
------
0 1726
1 220
Name: REFRIGERATED_LOCKER, dtype: int64
"""
Observations:
- Sample size for each option in all categorical variables are large enough for analysis (all contain above 200 observations)
Step 4: Categorical Variables: Email Domains
Purpose : email domains from clients can provide insight on which customers are more likely to open any email communications. For example, if the email used for subscription is a “junk” email, chances are this customer might not look at the inbox as often as we would like, as opposed to a professional email address where the customer might be looking at it multiple times a day. This can affect revenue since clients might order a meal after seeing an advertisement or a discount.
This step first selects the email domain for each customer, then creates a new categorical variable where each domain is classified as “personal”, “professional” or “junk”.
Finally, we will be one-hot encoding this new variable which will create three new columns for each email category. In these new columns, if an email corresponds to the column, that observation will take on the value 1.
# STEP 1: splitting emails
# placeholder list
placeholder_lst = []
# looping over each email address
for index, col in chef_org.iterrows():
# splitting email domain at '@'
split_email = chef_m.loc[index, 'EMAIL'].split(sep = '@')
# appending placeholder_lst with the results
placeholder_lst.append(split_email)
# converting placeholder_lst into a DataFrame
email_df = pd.DataFrame(placeholder_lst)
# STEP 2: concatenating with original DataFrame
# Creating a copy of chef for features and safety measure
chef = chef_m.copy()
# renaming column to concatenate
email_df.columns = ['name' , 'EMAIL_DOMAIN']
# concatenating personal_email_domain with chef DataFrame
chef = pd.concat([chef, email_df.loc[:, 'EMAIL_DOMAIN']],
axis = 1)
# printing value counts of personal_email_domain
chef.loc[: ,'EMAIL_DOMAIN'].value_counts()
# email domain types
professional_email_domains = ['@mmm.com', '@amex.com',
'@apple.com', '@boeing.com',
'@caterpillar.com', '@chevron.com',
'@cisco.com', '@cocacola.com',
'@disney.com', '@dupont.com',
'@exxon.com', '@ge.org',
'@goldmansacs.com', '@homedepot.com',
'@ibm.com', '@intel.com',
'@jnj.com', '@jpmorgan.com',
'@mcdonalds.com', '@merck.com',
'@microsoft.com', '@nike.com',
'@pfizer.com', '@pg.com',
'@travelers.com', '@unitedtech.com',
'@unitedhealth.com','@verizon.com',
'@visa.com', '@walmart.com']
personal_email_domains = ['@gmail.com', '@yahoo.com',
'@protonmail.com']
junk_email_domains = ['@me.com', '@aol.com',
'@hotmail.com', '@live.com',
'@msn.com', '@passport.com']
# placeholder list
placeholder_lst = []
# looping to group observations by domain type
for domain in chef['EMAIL_DOMAIN']:
if "@" + domain in professional_email_domains:
placeholder_lst.append('professional')
elif "@" + domain in personal_email_domains:
placeholder_lst.append('personal')
elif "@" + domain in junk_email_domains:
placeholder_lst.append('junk')
else:
print('Unknown')
# concatenating with original DataFrame
chef['email_domain_group'] = pd.Series(placeholder_lst)
# checking results and sample size
#print(chef['email_domain_group'].value_counts())
# Step 3: One-Hot encoding
one_hot_email_domain = pd.get_dummies(chef['email_domain_group'])
# dropping orginal columns to keep only encoded ones
chef_1 = chef.drop(['email_domain_group','EMAIL','EMAIL_DOMAIN'], axis = 1)
# joining encoded columns to dataset
chef_1 = chef_1.join(one_hot_email_domain)
# including new categorical variables to list
domains = ['professional','personal','junk']
categorical = categorical + domains
Step 5: Continuous Variables: Outliers Detection
Purpose: Outliers affect most predictive models. It increases variance in a variable, and therefore need to be flagged for two main reasons:
1) Using an outlier flag variable in our model quantifies the effect of that outlier on the variable we are trying to predict (in this case, revenue)
2) In some cases, removing outliers can improve our predictions and increase generalization of our model
In the following code, we visualize each variable’s distribution with an user-defined function and we look at the quartile ranges using descriptive statistics. We then set thresholds which will determine which observations are going to be considered as outliers in this analysis. Finally, we create a new column for each of the variables that contain outliers, where a 1 will be imputed for outlier observations.
Note: no outliers are removed in this part of the analysis
# Visualizing continuous variable distributions
for variable in continuous:
continuous_distributions(variable, chef_org, bins = 'fd', kde = True, rug = False)
Observations from distributions:
- Revenue:
- big dip in clients with revenue at approx 2,000
- Avg Time per Site Visit (in seconds):
- almost a normal distribution
- outliers after 200 (3.3 min)
- Followed Recommendations Percentage:
- outliers after 80%
- Average Preparation Video Time (in seconds):
- almost a normal distribution
- outliers after 250 (approx 4 min)
- Largest Order Size:
- almost normal distribution
- after 5: a family is usually 4 - 5 people, more than that it could be that these customers are throwing dinner parties or keeping the meals for the next day
- Median Meal Rating:
- no obvious outliers
- Average Clicks per visit:
- outliers before 10
## Visualizing count variable distributions
for variable in counts:
continuous_distributions(variable, chef_org, bins = 'auto',kde = False, rug = False)
Observations from distributions:
- Total Meals Ordered:
- strong dip in around 25 - investigate
- outliers after 320
- Unique Meals Purchased:
- outliers after 10
- Contacts with customer service:
- outliers after 13
- Product Categories Viewed:
- no obvious outliers
- Cancellations Before Noon:
- approx exponential distribution
- outliers after 8
- Cancellations After Noon:
- no obvious outliers
- Mobile Log-ins:
- no obvious outliers
- PC Log-ins:
- no obvious outliers
- Weekly Plan:
- no obvious outliers
- Early Deliveries:
- peak on 0
- no obvious outliers
- Late Deliveries:
- outliers after 17
- Master Class Attended:
- no obvious outliers
- Total Photos Viewed:
- peak on 0
- outliers after 800
# Establishing outliers thresholds for analysis
# Continous
avg_time_per_site_visit_hi = 200
avg_prep_vid_time_hi = 250
followed_rec_hi = 80
largest_order_size_hi = 5
avg_clicks_per_visit_lo = 10
# Counts:
total_meals_ordered_hi = 320
unique_meals_purchased_hi = 10
contacts_with_customer_service_hi = 13
cancellations_before_noon_hi = 8
late_deliveries_hi = 17
total_photos_viewed_hi = 800
# Target Variable
revenue_hi = 5500
# Creating Dictionary to link variables with outlier thresholds
lst_thresholds_hi = {
'AVG_TIME_PER_SITE_VISIT' : avg_time_per_site_visit_hi,
'AVG_PREP_VID_TIME' : avg_prep_vid_time_hi,
'TOTAL_MEALS_ORDERED' : total_meals_ordered_hi,
'UNIQUE_MEALS_PURCH' : unique_meals_purchased_hi,
'CONTACTS_W_CUSTOMER_SERVICE' : contacts_with_customer_service_hi,
'CANCELLATIONS_BEFORE_NOON' : cancellations_before_noon_hi,
'LATE_DELIVERIES' : late_deliveries_hi,
'TOTAL_PHOTOS_VIEWED' : total_photos_viewed_hi,
'REVENUE' : revenue_hi,
'FOLLOWED_RECOMMENDATIONS_PCT' : followed_rec_hi,
'LARGEST_ORDER_SIZE' : largest_order_size_hi
}
lst_thresholds_lo = {
'AVG_CLICKS_PER_VISIT' : avg_clicks_per_visit_lo
}
# Looping over variables to create outlier flags:
for key in lst_thresholds_hi.keys():
outlier_flag_hi(key,lst_thresholds_hi[key],chef_1)
for key in lst_thresholds_lo.keys():
outlier_flag_lo(key,lst_thresholds_lo[key],chef_1)
Step 6: Continuous/ Count Variables: Trend-Based Features
Purpose: Changes in variables behaviors in relation to our target variable can provide powerful explanations in our model as to how our revenue might be afftected.
In the following code, we visualize each variable’s relationship with revenue with an user-defined function. We then set thresholds which will determine which observations are going to be considered having a differing effect on our revenue. Finally, we create a new feature for each of the variables that contain this difference, where a 1 will be imputed for these observations.
# Defining dependent variables for trend analysis
dependent_vars = [
'AVG_TIME_PER_SITE_VISIT', 'FOLLOWED_RECOMMENDATIONS_PCT',
'AVG_PREP_VID_TIME', 'LARGEST_ORDER_SIZE',
'MEDIAN_MEAL_RATING', 'AVG_CLICKS_PER_VISIT',
'TOTAL_MEALS_ORDERED', 'UNIQUE_MEALS_PURCH',
'CONTACTS_W_CUSTOMER_SERVICE', 'PRODUCT_CATEGORIES_VIEWED',
'CANCELLATIONS_BEFORE_NOON', 'CANCELLATIONS_AFTER_NOON',
'MOBILE_LOGINS', 'PC_LOGINS',
'WEEKLY_PLAN', 'EARLY_DELIVERIES',
'LATE_DELIVERIES', 'MASTER_CLASSES_ATTENDED',
'TOTAL_PHOTOS_VIEWED'
]
# Visualizing dependent variable scatter plots in relation to Revenue
for variable in dependent_vars:
scatterplots(independ_var = variable, target_var = 'REVENUE', data = chef_org, color = 'r')
Observations from visualizations:
- Average Time per Site Visit
- different at 50 seconds
- 50 seconds to 200 seconds: no trend changes
- data scatters after 200
- outlier at 1600
- Followed recommendations percentage
- more dispersed after 70 percent
- Average prep video time
- more variance after 150s
- less variance after 210s
- after 300 less data points
- Largest order size
- increase in revenue until 5
- decrease but less steep after 5
- Median Meal Rating
- inflated at 3 and 4
- decrease after 4
- Average clicks per visit
- less than 8 very few data points
- increase in revenue until 10 clicks
- decrease after 10 until 15
- 16 to max constant
- Total Meals Ordered
- heteroskedasticity
- at 15 inflated
- increase at 100
- slower increase after 100
- Unique meals purchased
- inflated at 1: people must be ordering the same thing all the time
- until 9 - constant
- after 10 - outliers
- Contacts with customer service
- until 10: revenue increases
- after 10: revenue decreases
- Product Categories viewed
- until 5 slow decrease
- after 5 more constant
- Cancellations before noon
- after 8
- Cancellations after noon
- zero inflated
- at 3 - few observations with big revenue variance
- Mobile Logins
- 0 and 1 are increase
- 2 and 3 decrease
- PC Logins
- 4 to 6 increase
- 7 decrease
- Weekly plan
- after 15 seems to be a decrease
- constant after that
- Early deliveries
- no obvious trend changes (does not seem to be a problem)
- Late deliveries
- decrease until 8
- Master classes attended
- at 1
- at 2: less
- Total photos viewed
- 0 inflated
# Establishing outliers thresholds for analysis
# data scatters above this point
AVG_TIME_PER_SITE_VISIT_change_hi = 200
FOLLOWED_RECOMMENDATIONS_PCT_change_hi = 70
AVG_PREP_VID_TIME_change_lo = 150
AVG_PREP_VID_TIME_change_hi = 210
TOTAL_MEALS_ORDERED_change_hi = 100
# trend changes
LARGEST_ORDER_SIZE_change_hi = 5
AVG_CLICKS_PER_VISIT_change_lo = 8
AVG_CLICKS_PER_VISIT_change_hi = 16
UNIQUE_MEALS_PURCH_change_hi = 9
CONTACTS_W_CUSTOMER_SERVICE_change_hi = 10
PRODUCT_CATEGORIES_VIEWED_change_hi = 5
CANCELLATIONS_BEFORE_NOON_change_hi = 8
MOBILE_LOGINS_change_hi = 1
PC_LOGINS_change_hi = 6
WEEKLY_PLAN_change_hi = 15
LATE_DELIVERIES_change_lo = 8
TOTAL_MEALS_ORDERED_change_hi = 100
# Different at __
AVG_TIME_PER_SITE_VISIT_change_at = 50
MEDIAN_MEAL_RATING_change_at1 = 3
MEDIAN_MEAL_RATING_change_at2 = 4
MEDIAN_MEAL_RATING_change_at3 = 5
TOTAL_MEALS_ORDERED_change_at = 15
UNIQUE_MEALS_PURCH_change_at = 1
CANCELLATIONS_AFTER_NOON_change_at = 0
MASTER_CLASSES_ATTENDED_change_at1 = 1
MASTER_CLASSES_ATTENDED_change_at2 = 2
# Zero Inflated
TOTAL_PHOTOS_VIEWED_change_at = 0
# Creating Dictionary to link variables with trend thresholds
high_thresholds = {
'AVG_TIME_PER_SITE_VISIT' : [AVG_TIME_PER_SITE_VISIT_change_hi],
'FOLLOWED_RECOMMENDATIONS_PCT' : [FOLLOWED_RECOMMENDATIONS_PCT_change_hi],
'AVG_PREP_VID_TIME' : [AVG_PREP_VID_TIME_change_hi,
AVG_PREP_VID_TIME_change_lo],
'TOTAL_MEALS_ORDERED' : [TOTAL_MEALS_ORDERED_change_hi],
'LARGEST_ORDER_SIZE' : [LARGEST_ORDER_SIZE_change_hi],
'AVG_CLICKS_PER_VISIT' : [AVG_CLICKS_PER_VISIT_change_lo,
AVG_CLICKS_PER_VISIT_change_hi],
'UNIQUE_MEALS_PURCH' : [UNIQUE_MEALS_PURCH_change_hi],
'CONTACTS_W_CUSTOMER_SERVICE' : [CONTACTS_W_CUSTOMER_SERVICE_change_hi],
'PRODUCT_CATEGORIES_VIEWED' : [PRODUCT_CATEGORIES_VIEWED_change_hi],
'CANCELLATIONS_BEFORE_NOON' : [CANCELLATIONS_BEFORE_NOON_change_hi],
'MOBILE_LOGINS' : [MOBILE_LOGINS_change_hi],
'PC_LOGINS' : [PC_LOGINS_change_hi],
'WEEKLY_PLAN' : [WEEKLY_PLAN_change_hi],
'LATE_DELIVERIES' : [LATE_DELIVERIES_change_lo],
'TOTAL_MEALS_ORDERED' : [TOTAL_MEALS_ORDERED_change_hi]
}
at_thresholds = {
'AVG_TIME_PER_SITE_VISIT' : [AVG_TIME_PER_SITE_VISIT_change_at],
'MEDIAN_MEAL_RATING' : [MEDIAN_MEAL_RATING_change_at1,
MEDIAN_MEAL_RATING_change_at2,
MEDIAN_MEAL_RATING_change_at3],
'UNIQUE_MEALS_PURCH' : [UNIQUE_MEALS_PURCH_change_at],
'CANCELLATIONS_BEFORE_NOON' : [CANCELLATIONS_AFTER_NOON_change_at],
'MASTER_CLASSES_ATTENDED' : [MASTER_CLASSES_ATTENDED_change_at1,
MASTER_CLASSES_ATTENDED_change_at2],
'TOTAL_PHOTOS_VIEWED' : [TOTAL_PHOTOS_VIEWED_change_at]
}
# Looping over dataset to create trend based columns
for key, value in high_thresholds.items():
i = 0
for val in value:
higher_change_flag(key, i, val, chef_1)
i += 1
for key, value in at_thresholds.items():
i = 0
for val in value:
at_flag(key, i, val, chef_1)
i += 1
# Dropping variables after feature engineering
## !! only run this cell once !! ##
clean_chef = chef_1.drop([
'CROSS_SELL_SUCCESS',
'NAME',
'FIRST_NAME',
'FAMILY_NAME',
'm_FAMILY_NAME'
], axis = 1)
Part II: Transformations
Purpose: In preparation for modeling, it is important to prepare our dataset to the different modeling techniques by using transformation.
-
Explanatory variables: standardization is going to be applied to our dependent variables. This is important for models that use distance (variance) to predict the target variable, revenue. By standardizing, we ensure that all dependent variables are on the same scale and can be compared easily.
-
Target Variable: logarithmic is going to be applied to our independent variable. The distribution of revenue is skewed to the right. By treating this skewness with a log transformation, we normalize the magnitude of smaller and larger variables. In other words, lower revenues are expanded in our analysis and higher revenues are compressed. In addition, this transformation will decrease the effects of outliers which increases the application of any model to new unseen data.
Note: log transformations require non-zero values
Sources:
Feature Engineering for Machine Learning - Towards Data Science
Log Transformations for Skewed and Wide Distributions - Practical Data Science with R
#Defining a function to standardize numerical variables in the dataset:
def standard(num_df):
"""
This function standardizes a dataframe that contains variables which are either
integers or floats.
------
num_df : DataFrame, must contain only numerical variables
"""
# Isolating target variable from DF to be standardized
#num_df = num_df.drop(target_variable, axis = 1)
# INSTANTIATING a StandardScaler() object
scaler = StandardScaler()
# FITTING the scaler with housing_data
scaler.fit(num_df)
# TRANSFORMING our data after fit
X_scaled = scaler.transform(num_df)
# converting scaled data into a DataFrame
X_scaled_df = pd.DataFrame(X_scaled)
# adding labels to the scaled DataFrame
X_scaled_df.columns = num_df.columns
# Re-attaching target variable to DataFrame
#X_scaled_df = X_scaled_df.join(target_variable)
# returning the standardized data frame into the global environment
return X_scaled_df
Performing the log transformation of revenue:
# Log Transformation
# creating a copy for safety measures
clean_chef = clean_chef.copy()
#transforming only REVENUE column
clean_chef['rev_log'] = clean_chef['REVENUE'].transform(np.log)
Standardizing the dataset (without revenue):
# Standardization
# creating a copy for safety measures
clean_chef = clean_chef.copy()
# dropping revenue from standardization
chef_x = clean_chef.drop(['REVENUE','rev_log'], axis = 1)
#clean_chef.columns
chef_target = clean_chef.loc[:,['REVENUE','rev_log']]
# standardizing with user defined function and joining target revenue
chef_std = standard(chef_x).join(chef_target)
Part III: Modelling
Purpose: Find a model that can predict a new customer’s revenue.
The following dictionary format allows us to easily test different variable combinations. These are the the variables tested for each instance.
# Defining a dictionary with variables names for each different model test
variables_dict = {
"Base" : [ # will only work with chef_org
'REVENUE', 'CROSS_SELL_SUCCESS', 'NAME', 'EMAIL', 'FIRST_NAME',
'FAMILY_NAME', 'TOTAL_MEALS_ORDERED', 'UNIQUE_MEALS_PURCH',
'CONTACTS_W_CUSTOMER_SERVICE', 'PRODUCT_CATEGORIES_VIEWED',
'AVG_TIME_PER_SITE_VISIT', 'MOBILE_NUMBER', 'CANCELLATIONS_BEFORE_NOON',
'CANCELLATIONS_AFTER_NOON', 'TASTES_AND_PREFERENCES', 'PC_LOGINS',
'MOBILE_LOGINS', 'WEEKLY_PLAN', 'EARLY_DELIVERIES', 'LATE_DELIVERIES',
'PACKAGE_LOCKER', 'REFRIGERATED_LOCKER', 'FOLLOWED_RECOMMENDATIONS_PCT',
'AVG_PREP_VID_TIME', 'LARGEST_ORDER_SIZE', 'MASTER_CLASSES_ATTENDED',
'MEDIAN_MEAL_RATING', 'AVG_CLICKS_PER_VISIT', 'TOTAL_PHOTOS_VIEWED'
],
"Full_Features" : [
'REVENUE', 'TOTAL_MEALS_ORDERED', 'UNIQUE_MEALS_PURCH',
'CONTACTS_W_CUSTOMER_SERVICE', 'PRODUCT_CATEGORIES_VIEWED',
'AVG_TIME_PER_SITE_VISIT', 'MOBILE_NUMBER', 'CANCELLATIONS_BEFORE_NOON',
'CANCELLATIONS_AFTER_NOON', 'TASTES_AND_PREFERENCES', 'PC_LOGINS',
'MOBILE_LOGINS', 'WEEKLY_PLAN', 'EARLY_DELIVERIES', 'LATE_DELIVERIES',
'PACKAGE_LOCKER', 'REFRIGERATED_LOCKER', 'FOLLOWED_RECOMMENDATIONS_PCT',
'AVG_PREP_VID_TIME', 'LARGEST_ORDER_SIZE', 'MASTER_CLASSES_ATTENDED',
'MEDIAN_MEAL_RATING', 'AVG_CLICKS_PER_VISIT', 'TOTAL_PHOTOS_VIEWED',
'junk', 'personal', 'professional', 'out_AVG_TIME_PER_SITE_VISIT',
'out_AVG_PREP_VID_TIME', 'out_TOTAL_MEALS_ORDERED', 'out_UNIQUE_MEALS_PURCH',
'out_CONTACTS_W_CUSTOMER_SERVICE', 'out_CANCELLATIONS_BEFORE_NOON',
'out_LATE_DELIVERIES', 'out_TOTAL_PHOTOS_VIEWED', 'out_REVENUE',
'out_FOLLOWED_RECOMMENDATIONS_PCT', 'out_LARGEST_ORDER_SIZE',
'out_AVG_CLICKS_PER_VISIT', 'change_AVG_TIME_PER_SITE_VISIT_0',
'change_FOLLOWED_RECOMMENDATIONS_PCT_0','change_AVG_PREP_VID_TIME_0',
'change_AVG_PREP_VID_TIME_1', 'change_TOTAL_MEALS_ORDERED_0',
'change_LARGEST_ORDER_SIZE_0', 'change_AVG_CLICKS_PER_VISIT_0',
'change_AVG_CLICKS_PER_VISIT_1', 'change_UNIQUE_MEALS_PURCH_0',
'change_CONTACTS_W_CUSTOMER_SERVICE_0', 'change_PRODUCT_CATEGORIES_VIEWED_0',
'change_CANCELLATIONS_BEFORE_NOON_0', 'change_MOBILE_LOGINS_0',
'change_PC_LOGINS_0', 'change_WEEKLY_PLAN_0', 'change_LATE_DELIVERIES_0',
'change_MEDIAN_MEAL_RATING_0', 'change_MEDIAN_MEAL_RATING_1',
'change_MEDIAN_MEAL_RATING_2', 'change_MASTER_CLASSES_ATTENDED_0',
'change_MASTER_CLASSES_ATTENDED_1', 'change_TOTAL_PHOTOS_VIEWED_0'
],
"LinearReg Features" : [
'TOTAL_MEALS_ORDERED', 'CONTACTS_W_CUSTOMER_SERVICE', 'AVG_PREP_VID_TIME',
'LARGEST_ORDER_SIZE', 'TOTAL_PHOTOS_VIEWED',
'change_AVG_TIME_PER_SITE_VISIT_0',
'change_UNIQUE_MEALS_PURCH_0', 'change_CONTACTS_W_CUSTOMER_SERVICE_0',
'change_MEDIAN_MEAL_RATING_1','change_MASTER_CLASSES_ATTENDED_0',
'change_MASTER_CLASSES_ATTENDED_1'
],
"Log Revenue Features" : [
'REVENUE', 'TOTAL_MEALS_ORDERED', 'UNIQUE_MEALS_PURCH',
'CONTACTS_W_CUSTOMER_SERVICE', 'PRODUCT_CATEGORIES_VIEWED',
'AVG_TIME_PER_SITE_VISIT', 'MOBILE_NUMBER', 'CANCELLATIONS_BEFORE_NOON',
'CANCELLATIONS_AFTER_NOON', 'TASTES_AND_PREFERENCES', 'PC_LOGINS',
'MOBILE_LOGINS', 'WEEKLY_PLAN', 'EARLY_DELIVERIES', 'LATE_DELIVERIES',
'PACKAGE_LOCKER', 'REFRIGERATED_LOCKER', 'FOLLOWED_RECOMMENDATIONS_PCT',
'AVG_PREP_VID_TIME', 'LARGEST_ORDER_SIZE', 'MASTER_CLASSES_ATTENDED',
'MEDIAN_MEAL_RATING', 'AVG_CLICKS_PER_VISIT', 'TOTAL_PHOTOS_VIEWED',
'junk', 'personal', 'professional', 'out_AVG_TIME_PER_SITE_VISIT',
'out_AVG_PREP_VID_TIME', 'out_TOTAL_MEALS_ORDERED', 'out_UNIQUE_MEALS_PURCH',
'out_CONTACTS_W_CUSTOMER_SERVICE', 'out_CANCELLATIONS_BEFORE_NOON',
'out_LATE_DELIVERIES', 'out_TOTAL_PHOTOS_VIEWED', 'out_REVENUE',
'out_FOLLOWED_RECOMMENDATIONS_PCT', 'out_LARGEST_ORDER_SIZE',
'out_AVG_CLICKS_PER_VISIT', 'change_AVG_TIME_PER_SITE_VISIT_0',
'change_FOLLOWED_RECOMMENDATIONS_PCT_0','change_AVG_PREP_VID_TIME_0',
'change_AVG_PREP_VID_TIME_1', 'change_TOTAL_MEALS_ORDERED_0',
'change_LARGEST_ORDER_SIZE_0', 'change_AVG_CLICKS_PER_VISIT_0',
'change_AVG_CLICKS_PER_VISIT_1', 'change_UNIQUE_MEALS_PURCH_0',
'change_CONTACTS_W_CUSTOMER_SERVICE_0', 'change_PRODUCT_CATEGORIES_VIEWED_0',
'change_CANCELLATIONS_BEFORE_NOON_0', 'change_MOBILE_LOGINS_0',
'change_PC_LOGINS_0', 'change_WEEKLY_PLAN_0', 'change_LATE_DELIVERIES_0',
'change_MEDIAN_MEAL_RATING_0', 'change_MEDIAN_MEAL_RATING_1',
'change_MEDIAN_MEAL_RATING_2', 'change_MASTER_CLASSES_ATTENDED_0',
'change_MASTER_CLASSES_ATTENDED_1', 'change_TOTAL_PHOTOS_VIEWED_0','rev_log'
],
"Lasso Features" : [
'REVENUE', 'TOTAL_MEALS_ORDERED', 'UNIQUE_MEALS_PURCH',
'CONTACTS_W_CUSTOMER_SERVICE',
'AVG_TIME_PER_SITE_VISIT', 'CANCELLATIONS_BEFORE_NOON',
'CANCELLATIONS_AFTER_NOON', 'PC_LOGINS', 'MOBILE_LOGINS',
'EARLY_DELIVERIES', 'REFRIGERATED_LOCKER', 'AVG_PREP_VID_TIME',
'LARGEST_ORDER_SIZE',
'MEDIAN_MEAL_RATING', 'TOTAL_PHOTOS_VIEWED', 'junk',
'out_TOTAL_MEALS_ORDERED', 'out_UNIQUE_MEALS_PURCH',
'out_CONTACTS_W_CUSTOMER_SERVICE','out_LATE_DELIVERIES',
'out_TOTAL_PHOTOS_VIEWED', 'out_REVENUE', 'out_LARGEST_ORDER_SIZE',
'out_AVG_CLICKS_PER_VISIT','change_AVG_PREP_VID_TIME_1', 'change_LARGEST_ORDER_SIZE_0',
'change_UNIQUE_MEALS_PURCH_0', 'change_CONTACTS_W_CUSTOMER_SERVICE_0',
'change_PRODUCT_CATEGORIES_VIEWED_0','change_CANCELLATIONS_BEFORE_NOON_0',
'change_PC_LOGINS_0', 'change_WEEKLY_PLAN_0',
'change_MEDIAN_MEAL_RATING_0', 'change_MEDIAN_MEAL_RATING_1',
'change_MEDIAN_MEAL_RATING_2', 'change_MASTER_CLASSES_ATTENDED_0',
'change_MASTER_CLASSES_ATTENDED_1', 'change_TOTAL_PHOTOS_VIEWED_0','rev_log'
],
"ARD Features" : [
'REVENUE', 'TOTAL_MEALS_ORDERED', 'CONTACTS_W_CUSTOMER_SERVICE',
'AVG_PREP_VID_TIME', 'LARGEST_ORDER_SIZE',
'MEDIAN_MEAL_RATING', 'out_TOTAL_MEALS_ORDERED',
'out_CONTACTS_W_CUSTOMER_SERVICE',
'change_AVG_PREP_VID_TIME_1', 'change_UNIQUE_MEALS_PURCH_0',
'change_CONTACTS_W_CUSTOMER_SERVICE_0',
'change_MEDIAN_MEAL_RATING_0', 'change_MEDIAN_MEAL_RATING_1',
'change_MASTER_CLASSES_ATTENDED_0','change_MASTER_CLASSES_ATTENDED_1',
'change_TOTAL_PHOTOS_VIEWED_0','rev_log'
]
}
A) Base Linear Model
We’ll start with an multilinear model. We’ll be using the statsmodel package to print out comprehensive summary to better understand our features and how they relate to REVENUE:
Step 1: Correlation between dependent variables and independent variable
Step 2: OLS model with original features
Step 3: OLS model with original and engineered features
Step 4: OLS model with fitted variables (only significant variables)
Step 1: Correlation between dependent variables and independent variable
# creating a (Pearson) correlation matrix
df_corr = clean_chef.corr().round(2)
Step 2: OLS model with original features
# Creating a DataFrame with only Original Features (Base Model)
chef_org_explanatory = chef_org[variables_dict['Base']]
# dropping Revenue and Discrete variables from the explanatory variable set
chef_org_explanatory = chef_org_explanatory.drop(['REVENUE','NAME','FIRST_NAME','FAMILY_NAME', 'EMAIL'], axis = 1)
# Building a full OLS model with all original features
lm_full = smf.ols(formula = """ chef_org['REVENUE'] ~
chef_org['CROSS_SELL_SUCCESS'] +
chef_org['TOTAL_MEALS_ORDERED'] +
chef_org['UNIQUE_MEALS_PURCH'] +
chef_org['CONTACTS_W_CUSTOMER_SERVICE'] +
chef_org['PRODUCT_CATEGORIES_VIEWED'] +
chef_org['AVG_TIME_PER_SITE_VISIT'] +
chef_org['MOBILE_NUMBER'] +
chef_org['CANCELLATIONS_BEFORE_NOON'] +
chef_org['CANCELLATIONS_AFTER_NOON'] +
chef_org['TASTES_AND_PREFERENCES'] +
chef_org['PC_LOGINS'] +
chef_org['MOBILE_LOGINS'] +
chef_org['WEEKLY_PLAN'] +
chef_org['EARLY_DELIVERIES'] +
chef_org['LATE_DELIVERIES'] +
chef_org['PACKAGE_LOCKER'] +
chef_org['REFRIGERATED_LOCKER'] +
chef_org['FOLLOWED_RECOMMENDATIONS_PCT'] +
chef_org['AVG_PREP_VID_TIME'] +
chef_org['LARGEST_ORDER_SIZE'] +
chef_org['MASTER_CLASSES_ATTENDED'] +
chef_org['MEDIAN_MEAL_RATING'] +
chef_org['AVG_CLICKS_PER_VISIT'] +
chef_org['TOTAL_PHOTOS_VIEWED']
""",
data = chef_org)
# telling Python to run the data through the blueprint
results_full = lm_full.fit()
# printing the results
print(results_full.summary2())
Observations:
- F-statistic p-value is very low: model is explaining (to a certain degree) the REVENUE
- a lot of statistically insignificant variables that might be adding noise to our model
- significant variables: total meals ordered (+ 5.7), unique meal purchased (-63.7), contacts with customer service (+ 45.6), average prep video time (+ 9.3), largest order size (- 96), master classes attended (+ 175.2), median meal rating ( + 342.4), total photos viewed (+ 0.69).
- from these, it is not surprising to have total meals ordered and largest order size as revenue = quantity * price and these variables are directly related to quantity. However it is interesting to look at unique meals purchased having a negative relationship with revenue. This could indicate that customers for Apprentice Chef are most likely to be always ordering the same meals. –> for further investigation
- ! The condition number is large (6e+03). This might indicate strong multicollinearity or other numerical problems.
Step 3: OLS model with original and engineered features
### Creating a Feature Rich DataFrame (Full model)
chef_full_explanatory = clean_chef[variables_dict['Full_Features']]
# dropping Revenue and Discrete variables from the explanatory variable set
chef_full_explanatory = chef_full_explanatory.drop(['REVENUE','out_REVENUE'], axis = 1)
## Building a full OLS model with created features
lm_full = smf.ols(formula = """ chef_org['REVENUE'] ~
clean_chef['TOTAL_MEALS_ORDERED'] +
clean_chef['UNIQUE_MEALS_PURCH'] +
clean_chef['CONTACTS_W_CUSTOMER_SERVICE'] +
clean_chef['PRODUCT_CATEGORIES_VIEWED'] +
clean_chef['AVG_TIME_PER_SITE_VISIT'] +
clean_chef['MOBILE_NUMBER'] +
clean_chef['CANCELLATIONS_BEFORE_NOON'] +
clean_chef['CANCELLATIONS_AFTER_NOON'] +
clean_chef['TASTES_AND_PREFERENCES'] +
clean_chef['PC_LOGINS'] +
clean_chef['MOBILE_LOGINS'] +
clean_chef['WEEKLY_PLAN'] +
clean_chef['EARLY_DELIVERIES'] +
clean_chef['LATE_DELIVERIES'] +
clean_chef['PACKAGE_LOCKER'] +
clean_chef['REFRIGERATED_LOCKER'] +
clean_chef['FOLLOWED_RECOMMENDATIONS_PCT'] +
clean_chef['AVG_PREP_VID_TIME'] +
clean_chef['LARGEST_ORDER_SIZE'] +
clean_chef['MASTER_CLASSES_ATTENDED'] +
clean_chef['MEDIAN_MEAL_RATING'] +
clean_chef['AVG_CLICKS_PER_VISIT'] +
clean_chef['TOTAL_PHOTOS_VIEWED'] +
clean_chef['junk'] +
clean_chef['personal'] +
clean_chef['professional'] +
clean_chef['out_AVG_TIME_PER_SITE_VISIT'] +
clean_chef['out_AVG_PREP_VID_TIME'] +
clean_chef['out_TOTAL_MEALS_ORDERED'] +
clean_chef['out_UNIQUE_MEALS_PURCH'] +
clean_chef['out_CONTACTS_W_CUSTOMER_SERVICE'] +
clean_chef['out_CANCELLATIONS_BEFORE_NOON'] +
clean_chef['out_LATE_DELIVERIES'] +
clean_chef['out_TOTAL_PHOTOS_VIEWED'] +
clean_chef['out_FOLLOWED_RECOMMENDATIONS_PCT'] +
clean_chef['out_LARGEST_ORDER_SIZE'] +
clean_chef['out_AVG_CLICKS_PER_VISIT'] +
clean_chef['change_AVG_TIME_PER_SITE_VISIT_0'] +
clean_chef['change_FOLLOWED_RECOMMENDATIONS_PCT_0'] +
clean_chef['change_AVG_PREP_VID_TIME_0'] +
clean_chef['change_AVG_PREP_VID_TIME_1'] +
clean_chef['change_TOTAL_MEALS_ORDERED_0'] +
clean_chef['change_LARGEST_ORDER_SIZE_0'] +
clean_chef['change_AVG_CLICKS_PER_VISIT_0'] +
clean_chef['change_AVG_CLICKS_PER_VISIT_1'] +
clean_chef['change_UNIQUE_MEALS_PURCH_0'] +
clean_chef['change_CONTACTS_W_CUSTOMER_SERVICE_0'] +
clean_chef['change_PRODUCT_CATEGORIES_VIEWED_0'] +
clean_chef['change_CANCELLATIONS_BEFORE_NOON_0'] +
clean_chef['change_MOBILE_LOGINS_0'] +
clean_chef['change_PC_LOGINS_0'] +
clean_chef['change_WEEKLY_PLAN_0'] +
clean_chef['change_LATE_DELIVERIES_0'] +
clean_chef['change_MEDIAN_MEAL_RATING_0'] +
clean_chef['change_MEDIAN_MEAL_RATING_1'] +
clean_chef['change_MEDIAN_MEAL_RATING_2'] +
clean_chef['change_MASTER_CLASSES_ATTENDED_0'] +
clean_chef['change_MASTER_CLASSES_ATTENDED_1'] +
clean_chef['change_TOTAL_PHOTOS_VIEWED_0']
""",
data = clean_chef)
# telling Python to run the data through the blueprint
results_full = lm_full.fit()
# printing the results
#print(results_full.summary2())
Observations:
- improved adjusted r-squared: features created help explain REVENUE better
- still a lot of insignificant features
- high possibility of multicollinearity
Step 4: OLS model with fitted variables (only significant variables)
## Creating a DataFrame with only significant features
chef_fit = clean_chef[variables_dict['LinearReg Features']]
# Building a fit OLS model based on P-value from full model (alpha = 0.001)
lm_fit = smf.ols(formula = """ chef_org['REVENUE'] ~
clean_chef['TOTAL_MEALS_ORDERED'] +
clean_chef['CONTACTS_W_CUSTOMER_SERVICE'] +
clean_chef['AVG_PREP_VID_TIME'] +
clean_chef['LARGEST_ORDER_SIZE'] +
clean_chef['TOTAL_PHOTOS_VIEWED'] +
clean_chef['change_AVG_TIME_PER_SITE_VISIT_0'] +
clean_chef['change_UNIQUE_MEALS_PURCH_0'] +
clean_chef['change_CONTACTS_W_CUSTOMER_SERVICE_0'] +
clean_chef['change_MEDIAN_MEAL_RATING_1'] +
clean_chef['change_MASTER_CLASSES_ATTENDED_0'] +
clean_chef['change_MASTER_CLASSES_ATTENDED_1']
""",
data = clean_chef)
# telling Python to run the data through the blueprint
results_fit = lm_fit.fit()
# printing the results
print(results_fit.summary2())
Observations:
- skewness reduced
- adjusted r-squared reduced: normal since this is the first fitted model!
- all variables are significant
Let’s first run a linear regression model on sklearn to evaluate our training and testing score:
# applying modeling with scikit-learn
# INSTANTIATING a model object
lr = LinearRegression()
# FITTING to the training data
lr_fit = lr.fit(X_train, y_train)
# PREDICTING on new data
lr_pred = lr_fit.predict(X_test)
# SCORING the results
print('Training Score:', lr.score(X_train, y_train).round(4))
print('Testing Score:', lr.score(X_test, y_test).round(4))
# saving results for later:
lr_train_score = lr.score(X_train, y_train).round(4)
lr_test_score = lr.score(X_test, y_test).round(4)
Training Score: 0.8376
Testing Score: 0.7873
Observations:
- not a bad testing score!
- we can improve it through feature selection methods
B) Feature Selection
In this section, we’ll be utilizing different methods to improve our models predictive power by shedding a light on which features are important:
Method 1: L1 Regularization or Lasso
The goal is to evaluate which features are important to our target variable. The model uses a penalty function to decrease a feature’s coefficient each time it runs, thus making insignificant coefficients equal to zero by the end.
Its parameters specified below are alpha (regularization parameter, when equal to one - simple linear regression, as it reduces, we further filter our features by penalizing them) and normalize (which here is set to false since we are using normalized data on it). It is important to use standardized data with this method.
We then look at the coefficients for each of the variables to identify features that are important.
sources:
L1 and L2 Regularization Methods - Towards Data Science
Ridge and Lasso Regression - Towards Data Science
Preparation:
- random state: seed set to 222
- test size: 0.25
- features: orignial and engineered features
- revenue: log
## Preparing the orginal data for SKLEARN models
# Creating a variable for random seed
seed = 222
# Preparing response variable
chef_target = clean_chef['rev_log']
### Non-transformed Data ###
# Preparing x-variables
## use dictionary keys for different sets of features (might need to drop different columns)
chef_x = clean_chef[variables_dict['Log Revenue Features']].drop(['REVENUE','rev_log'], axis = 1)# 'out_REVENUE',
# Running train/test split
X_train, X_test, y_train, y_test = train_test_split(
chef_x,
chef_target,
test_size = 0.25,
random_state = seed)
### Transformed Data ####
# Preparing x-variables
chef_std_x = chef_std[variables_dict['Log Revenue Features']].drop(['REVENUE','rev_log'], axis = 1) #'out_REVENUE',
# Running train/test split
X_train_s, X_test_s, y_train_s, y_test_s = train_test_split(
chef_std_x,
chef_target,
test_size = 0.25,
random_state = seed)
Now let’s run our first regularization model on sklearn: Lasso (L1 Regularization).
First pass through lasso model with normalized data:
# INSTANTIATING a model object
lasso_model = sklearn.linear_model.Lasso(alpha = 0.003,
normalize = False) # using standardized data
# FITTING the training data
lasso_fit = lasso_model.fit(X_train_s, y_train_s)
# PREDICTING on new data
lasso_pred = lasso_fit.predict(X_test_s)
print('Training Score:', lasso_model.score(X_train_s, y_train_s).round(4))
print('Testing Score:', lasso_model.score(X_test_s, y_test_s).round(4))
Training Score: 0.825
Testing Score: 0.7817
With the Lasso model, we are most interested in the coefficients of different variables. Coefficients with 0 are insignificant for our target variable.
# storing coefficients as df
lasso_model_coef = pd.DataFrame(lasso_model.coef_)
# naming variables to coefficients
lasso_model_coef['Variable Names'] = chef_std_x.columns
# Looking at insignificant coefficients
drop = lasso_model_coef.iloc[:,:][lasso_model_coef[0] == 0]
Observations: significant features:
- TOTAL_MEALS_ORDERED
- UNIQUE_MEALS_PURCH
- CONTACTS_W_CUSTOMER_SERVICE
- AVG_TIME_PER_SITE_VISIT
- CANCELLATIONS_BEFORE_NOON
- CANCELLATIONS_AFTER_NOON
- PC_LOGINS
- MOBILE_LOGINS
- EARLY_DELIVERIES
- REFRIGERATED_LOCKER
- AVG_PREP_VID_TIME
- LARGEST_ORDER_SIZE
- MEDIAN_MEAL_RATING
- TOTAL_PHOTOS_VIEWED
- junk
- outlier flags: out_TOTAL_MEALS_ORDERED, out_UNIQUE_MEALS_PURCH, out_CONTACTS_W_CUSTOMER_SERVICE, out_LATE_DELIVERIES, out_TOTAL_PHOTOS_VIEWED, out_REVENUE, out_LARGEST_ORDER_SIZE, out_AVG_CLICKS_PER_VISIT,
- trend-based flags: change_AVG_PREP_VID_TIME_1, change_LARGEST_ORDER_SIZE_0, change_UNIQUE_MEALS_PURCH_0, change_CONTACTS_W_CUSTOMER_SERVICE_0, change_PRODUCT_CATEGORIES_VIEWED_0,change_CANCELLATIONS_BEFORE_NOON_0, change_PC_LOGINS_0, change_WEEKLY_PLAN_0, change_MEDIAN_MEAL_RATING_0, change_MEDIAN_MEAL_RATING_1, change_MEDIAN_MEAL_RATING_2, change_MASTER_CLASSES_ATTENDED_0, change_MASTER_CLASSES_ATTENDED_1, change_TOTAL_PHOTOS_VIEWED_0
Observations: - we can see that this method has yielded a large number of variables, which reduces the interpretability of our model.
Method 2: L2 Regularization or Bayesian Ridge Regression
Now let’s run our another regularization model on sklearn: ARDRegression (L2 Regularization). The goal is to evaluate which features are important to our target variable. The model uses a penalty function to decrease a feature’s coefficient each time it runs, thus making insignificant coefficients equal to zero by the end. With this method, our lambda (L2) is treated as a variable, and is much more adaptable to our data.
Its parameters specified below are n_iter (number of maximum interations) and normalize (which here is set to false since we are using normalized data on it). It is important to use standardized data with this method.
We then look at the coefficients for each of the variables to identify features that are important.
sources:
L1 and L2 Regularization Methods - Towards Data Science
ARD Regression - scikit-learn package documentation
# INSTANTIATING a model object
ard_model = sklearn.linear_model.ARDRegression(n_iter = 400,
normalize = False) # using standardized data
# FITTING the training data
ard_fit = ard_model.fit(X_train_s, y_train_s)
# PREDICTING on new data
ard_pred = ard_fit.predict(X_test_s)
print('Training Score:', ard_model.score(X_train_s, y_train_s).round(4))
print('Testing Score:', ard_model.score(X_test_s, y_test_s).round(4))
Training Score: 0.8258
Testing Score: 0.7837
# storing coefficients as df
ard_model_coef = pd.DataFrame(ard_model.coef_)
ard_model_coef['Variable Names'] = chef_std_x.columns
# Looking at insignificant coefficients
drop = ard_model_coef.iloc[:,:][ard_model_coef[0] == 0]
Observations:
significant features:
- TOTAL_MEALS_ORDERED
- CONTACTS_W_CUSTOMER_SERVICE
- AVG_PREP_VID_TIME
- LARGEST_ORDER_SIZE
- MEDIAN_MEAL_RATING
- out_TOTAL_MEALS_ORDERED
- out_CONTACTS_W_CUSTOMER_SERVICE
- change_AVG_PREP_VID_TIME_1
- change_UNIQUE_MEALS_PURCH_0
- change_CONTACTS_W_CUSTOMER_SERVICE_0
- change_MEDIAN_MEAL_RATING_0
- change_MEDIAN_MEAL_RATING_1
- change_MASTER_CLASSES_ATTENDED_0
- change_MASTER_CLASSES_ATTENDED_1
- change_TOTAL_PHOTOS_VIEWED_0
We can see the second method has further filtered through our variables, creating a much simpler model.
C) Model Selection
In this section, we’ll evaluate the performance of the linear regression and the KNN regression models against each other, using the feautures selected with regularization methods.
Preparation:
- random state: seed set to 222
- test size: 0.25
- features: ARD selected features
- revenue: log
## Preparing the orginal data for SKLEARN models
# Creating a variable for random seed
seed = 222
# Preparing response variable
chef_target = clean_chef['rev_log']
### Non-transformed Data ###
# Preparing x-variables
## use dictionary keys for different sets of features (might need to drop different columns)
chef_x = clean_chef[variables_dict['ARD Features']].drop(['REVENUE','rev_log'], axis = 1)# 'out_REVENUE',
# Running train/test split
X_train, X_test, y_train, y_test = train_test_split(
chef_x,
chef_target,
test_size = 0.25,
random_state = seed)
### Transformed Data ####
# Preparing x-variables
chef_std_x = chef_std[variables_dict['ARD Features']].drop(['REVENUE','rev_log'], axis = 1) #'out_REVENUE',
# Running train/test split
X_train_s, X_test_s, y_train_s, y_test_s = train_test_split(
chef_std_x,
chef_target,
test_size = 0.25,
random_state = seed)
Model 1: OLS (linear regression - ordinary least squares)
# applying modeling with scikit-learn
# INSTANTIATING a model object
lr = LinearRegression()
# FITTING to the training data
lr_fit = lr.fit(X_train, y_train)
# PREDICTING on new data
lr_pred = lr_fit.predict(X_test)
# SCORING the results
print('Training Score:', lr.score(X_train, y_train).round(4))
print('Testing Score:', lr.score(X_test, y_test).round(4))
# saving results for later:
lr_train_score = lr.score(X_train, y_train).round(4)
lr_test_score = lr.score(X_test, y_test).round(4)
Training Score: 0.8259
Testing Score: 0.7832
Model 2: K-Nearest Neighbors Regression To best utilize this model, we need to include a calculation of the optimal number of neighbors. We do so through a loop, that evaluates n neighbors from 1 to 21.
# creating lists for training set accuracy and test set accuracy
training_accuracy = []
test_accuracy = []
# building a visualization of 1 to 50 neighbors
neighbors_settings = range(1, 21)
for n_neighbors in neighbors_settings:
# Building the model
clf = KNeighborsRegressor(n_neighbors = n_neighbors)
clf.fit(X_train_s, y_train_s)
# Recording the training set accuracy
training_accuracy.append(clf.score(X_train_s, y_train_s))
# Recording the generalization accuracy
test_accuracy.append(clf.score(X_test_s, y_test_s))
# finding the optimal number of neighbors
opt_neighbors = test_accuracy.index(max(test_accuracy)) + 1
print(f"""The optimal number of neighbors is {opt_neighbors}""")
# Model:
# INSTANTIATING a KNN model object
knn_reg = KNeighborsRegressor(algorithm = 'auto',
n_neighbors = opt_neighbors)
# FITTING to the training data
knn_reg.fit(X_train_s, y_train_s)
# PREDICTING on new data
knn_reg_pred = knn_reg.predict(X_test_s)
# SCORING the results
print('Training Score:', knn_reg.score(X_train_s, y_train_s).round(4))
print('Testing Score:', knn_reg.score(X_test_s, y_test_s).round(4))
The optimal number of neighbors is 8
Training Score: 0.8499
Testing Score: 0.7849
Observations:
- KNN model score is slightly higher than a Linear model with features selected by regularization methods
- KNN slightly overfits our model (difference of 0.065 between train and test scores)
Conclusion: Linear model provides a slightly lower score with features selected by regularization methods. However, its interpretability will provide powerful business insights. However, we need to make sure we are meeting all the assumptions necessary of a linear model.
Part IV: Evaluating Model - Linear Model Assumptions
- Residual plots (is linear assumption valid? are outliers affecting our predictions?)
- Multicollinearity (highly correlated explanatory variables)
- Re - sampling methods (cross validation)
1. Residual Plot
# setting figure size
fig, ax = plt.subplots(figsize = (10, 10))
# developing a residual plot
sns.residplot(x = lr_pred, # prediction values
y = y_test) # actual values
# displaying the plot
plt.show()
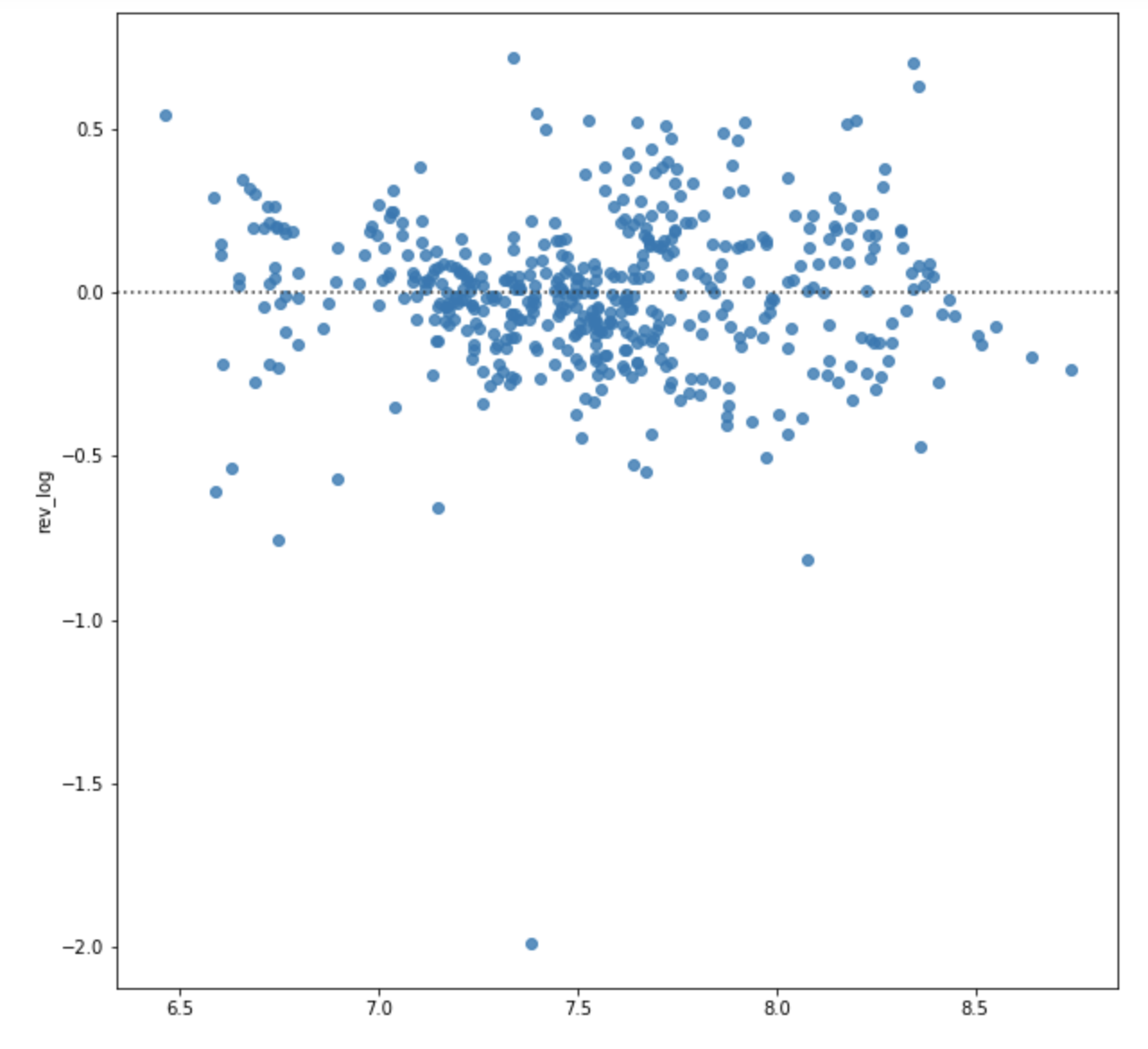
Observations:
- no obvious patterns: homoskedasticity assumption met, linear relationship met
- Caution: very big outlier could be affecting our prediction
sources:
Interpreting Log Transformations in a Linear Model
Interpreting Residual Plots to Improve your Regression
2. Evaluating Outlier Affect on Model
Variables in our model with outliers:
- Total meals ordered
- Largest order size
- Contact with customer service
- Avg prep video time
- Largest order size
Important: Since we are removing outliers, it is important to check how many observations we are removing from our dataset.
# Creating a copy of dataset for safety measure
out_chef = clean_chef.copy()
# Printing out size of dataframe with all data points
print(out_chef.shape)
# Subsetting outliers from our linear model features by using flags
out_chef = out_chef.loc[:][out_chef['out_TOTAL_MEALS_ORDERED'] == 0]
# Printing out size of dataframe after removing outliers
print(out_chef.shape)
(1946, 62)
(1939, 62)
Removed only 7 observations that we outliers in Total Meals Ordered. Total meals ordered is a variable that has a direct relationship with revenue since Revenue = Quantity x Price and Total meals ordered for each customer corresponds to its quantity. Therefore, any outliers could be affecting our model’s ability to generalize and predict new data.
# Re-running our linear model without outliers to compare test scores (previous = 0.7832)
# Preparing response variable
out_chef_target = out_chef['rev_log']
### Non-transformed Data ###
# Preparing x-variables
out_chef_x = out_chef[variables_dict['ARD Features']].drop(['REVENUE','rev_log','out_TOTAL_MEALS_ORDERED'],
axis = 1)# 'out_REVENUE',
# Running train/test split
X_train_out, X_test_out, y_train_out, y_test_out = train_test_split(
out_chef_x,
out_chef_target,
test_size = 0.25,
random_state = seed)
# applying modeling with scikit-learn
# INSTANTIATING a model object
out_lr = LinearRegression()
# FITTING to the training data
out_lr_fit = out_lr.fit(X_train_out, y_train_out)
# PREDICTING on new data
out_lr_pred = out_lr_fit.predict(X_test_out)
# SCORING the results
print('Training Score:', out_lr.score(X_train_out, y_train_out).round(4))
print('Testing Score:', out_lr.score(X_test_out, y_test_out).round(4))
# saving results for later:
out_lr_train_score = out_lr.score(X_train_out, y_train_out).round(4)
out_lr_test_score = out_lr.score(X_test_out, y_test_out).round(4)
Training Score: 0.807
Testing Score: 0.8279
Observations:
- outliers were having a large effect on model: new testing score = 0.8279
Let’s plot again our residual plot:
# setting figure size
fig, ax = plt.subplots(figsize = (10, 10))
# developing a residual plot
sns.residplot(x = out_lr_pred, # prediction values
y = y_test_out) # actual values
# displaying the plot
plt.show()
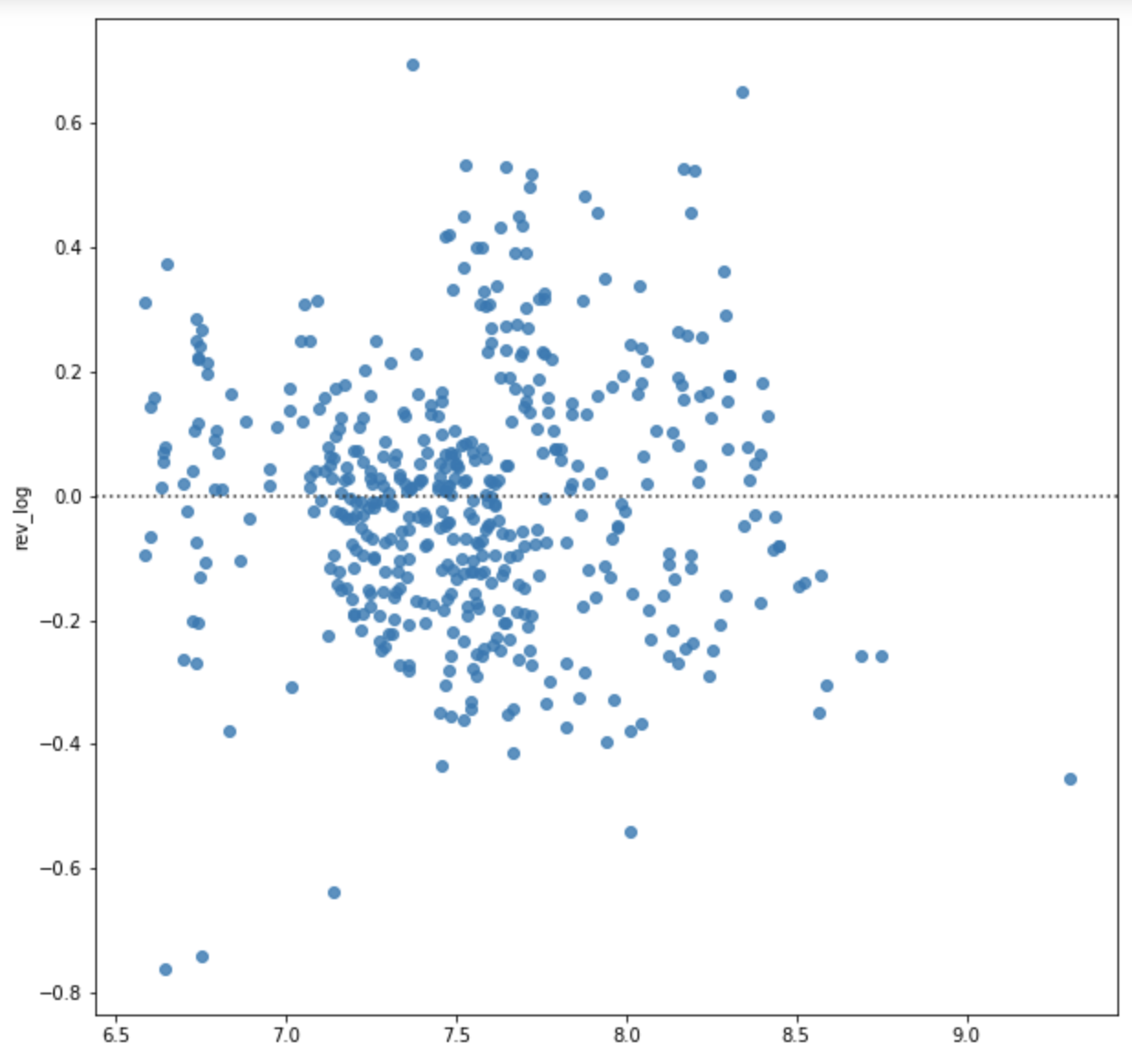
Observations:
- there still seems to be a few outliers in our model with really big residual. It is most likely these outlier do not come from our independent variables, and is instead an outlier in Revenue, which is why our model’s testing score still increased.
- for the purpose of this analysis, we will keep the Revenue outliers in our data, since the objective is to identify the best features to predict revenue for a new consumer. Further investigation is needed on this Revenue data point as to understand its relationship in with the selected features.
3. Multicollinearity
Multicollinearity occurs when variables used to predict a target variable are highly correlated amongst themselves. It can be affecting our model since we are double counting, leading to bad predictions and higher standard errors.
Because our model does not have many features, we can use a correlation matrix to identify which variables (if any) are higher correlated.
# correlation matrix
#fig, ax = plt.subplots(figsize=(15,15))
# defining data frame with utilized variables
corr_chef = out_chef.loc[:, variables_dict['ARD Features']].drop(['REVENUE','rev_log'], axis = 1).corr().round(2)
sns.heatmap(corr_chef,
cmap = 'coolwarm',
square = True,
annot = True,
linecolor = 'black',
linewidths = 0.5)
plt.show()
Observations:
- there are no correlations above 0.8 so we can say that multicollinearity is not affecting our model.
4. Re-sampling
Model performance is dependent on how we split train and testing. Therefore it is important to conduct cross-validation to understand how our model is capable of generalizing when seeing new data.
source: DataCamp - Supervised Learning with Scikit-Learn
# Using cross_val_score to store results of cross validation
cv_results = cross_val_score(out_lr, out_chef_x, out_chef_target, cv = 25)
np.mean(cv_results)
# creating lists for cross validation score results
cross_val = []
# building a visualization for different fold numbers
cross_val_settings = range(2, 30)
for n_folds in cross_val_settings:
# Building the model
cv_results = cross_val_score(out_lr, out_chef_x, out_chef_target, cv = n_folds)
# Recording the scores
cross_val.append(np.mean(cv_results))
# plotting the visualization
fig, ax = plt.subplots(figsize=(12,8))
plt.plot(cross_val_settings, cross_val, label = "Cross Validation Scores")
plt.ylabel("score")
plt.xlabel("number of folds")
plt.legend()
plt.show()
# finding the optimal number of neighbors
max_score = cross_val.index(max(cross_val)) + 1
print(f"""The max score was achieved at {max_score}""")
The max score was achieved at 11
# Finding the highest achieved test score with cross validation
cross_val[11]
0.8076273527253071
Observations:
- After cross-validation, our model still seems to perform really well to predict Revenue!
Conclusion
- Our best performing model was a Linear Regression with 15 features with a test score of 0.8279 and a cross validation score with 11 folds at 0.8086
- Optimal features were found using regularization methods such as Lasso and ARD Regression
- It is predicting the log of revenue, therefore when interpreting coefficients, it is important to transform back using 10(coef)
Business Insights
- Customer Segmentation
Even though we might think customers use meal kits for new recipes, our customer data shows that, all else equal, customers that order the same meals every time have a 71.24% higher revenue contribution than those who order different options.
This could mean a segmentation in terms of our customers purchase intentions:
1) customers that order our service for the practicality of quick and healthy meals
2) customers that order our service to increase their cooking skills
Indeed, customers that attend 2 master classes for instance have a 12.45% increase in revenue.
- Customer Service
Customers call customer service for a change in order delivery or a complaint. However,cancellations and calls are not correlated in our customer dataset, confirming Customer Service team’s observations.
Our ability to handle these complaints is somewhat effective. Until 10 calls, customers that have contacted customer services have an increase in revenue contribution of around 5%. However, after a customer has made 10 calls, their revenue contribution lowers by almost half (48%).
Recommendations and Business Implementation
Marketing
By identifying which customers belong to each of the segments identified above, we could use targeted marketing campaigns on emails or social media to improve number of orders. For example, sending discounts for master classes to those who order a variety of meals, whereas for those who always order the same meal, we could offer campaigns such as: ‘order 5 meals, get 1 free’.
Quick Re-order
Customers that always order the same meal seem to be our biggest customer segment. If we identify a customer as someone that orders always the same dish, we could include a ‘quick re-order’ button in our website and mobile app. This customer would be able to quickly order with 1 click.
Customer Service Data Collection
Due to competitive nature of this market, customer retention is key. When a customer has a bad experience with our delivery, they could easily switch to another service, food delivery or grocery stores. However, our data for customer service calls is insufficient to evaluate how many of our calls are complaints.
We should identify if a customer service call was a complaint or not. This provides extremely valuable insight on how a customer complaint affects our revenue, which would indirectly increase our competitive advantage.

